Định lý Viet của phương trình bậc hai và phương trình bậc ba

Vào khoảng chừng đầu thế kỉ loại XVII thì ngôi nhà Toán học tập tài phụ thân người Pháp François Viète đang được dò xét đi ra ông tơ contact trong những nghiệm với những thông số của phương trình bậc nhì.

Cái tuy nhiên thời buổi này tất cả chúng ta vẫn gọi là định lý / hệ thức Viet (Vi-Ét)!

Bạn đang xem: Định lý Viet của phương trình bậc hai và phương trình bậc ba

Tên gọi này là trọn vẹn thích hợp vì như thế nó vừa phải có trách nhiệm vừa phải ghi ghi nhớ công huân của những người đang được dò xét đi ra nó. Và ở vô nội dung bài viết ngày thời điểm ngày hôm nay, tất cả chúng ta tiếp tục bên nhau tuyên bố lại lăm le lý Viet và dò xét hiểu tăng một trong những phần mềm thông thường bắt gặp của lăm le lý này nhé !

I. Định lý Viet của phương trình bậc hai

Nếu $x_1, x_2$ là nhì nghiệm của phương trình bậc nhì $ax^2+bx+c=0$ thì $\left\{\begin{array}{ll}x_1+x_2&=\frac{-b}{a} \\ x_1x_2&=\frac{c}{a}\end{array}\right.$

II. Định lý Viet (Vi-Ét) của phương trình bậc ba

Nếu $x_1, x_2, x_3$ là phụ thân nghiệm của phương trình bậc phụ thân $ax^3+bx^2+cx+d=0$ thì $\left\{\begin{array}{ll}x_1+x_2+x_3&=\frac{-b}{a} \\ x_1x_2+x_1x_3+x_2x_3&=\frac{c}{a} \\ x_1x_2x_3&=\frac{-d}{a}\end{array}\right.$

III. Định lý Viet đích thị với …

IV. Một số phần mềm thông thường bắt gặp của lăm le lý Viet

Định lý Viet của phương trình bậc phụ thân và những bậc cao hơn nữa thì tất cả chúng ta tiếp tục không nhiều bắt gặp rộng lớn, giản dị là vì như thế bọn chúng không nhiều được phần mềm vô công tác Toán học tập Trung học tập.

Vậy nên ở nội dung bài viết này tôi chỉ triệu tập chỉ dẫn mang lại lăm le lý Viet của phương trình bậc nhì thôi nha chúng ta.

Định lý Viet của phương trình bậc hai với thật nhiều phần mềm trong các việc giải bài bác tập dượt, bên dưới đó là một trong những phần mềm chi biểu:

• Nhẩm nghiệm của phương trình.
• Tìm nhì số lúc biết tổng và tích.
• Tính độ quý hiếm biểu thức (biểu thức hoàn toàn có thể trình diễn trở nên nhiều thức đối xứng).
• Giải hệ phương trình đối xứng.
• Xét vệt của những nghiệm.

#1. Nhẩm nghiệm của phương trình

Ví dụ 1. Giải phương trình $x^2+2x-3=0$

Lời giải:

Vì phương trình bậc nhì đang được mang lại với $1+2+(-3)=0$ nên $x_1=\frac{1}{1}=1, x_2=\frac{-3}{1}=-3$

Vậy phương trình bậc nhì đang được mang lại với nhì nghiệm phân biệt là $1, -3$

Nhận xét: Ngoài cách thức dùng hệ ngược của lăm le lý Viet thì tất cả chúng ta còn thật nhiều cách thức nhằm giải phương trình bậc nhì này (tính $\Delta$, tính $\Delta’$, đồ dùng thị, …). Tuy nhiên cách thức bên trên là tối ưu nhất !

#2. Tìm nhì số lúc biết tổng và tích

Cho nhì số thức $a, b$ ngẫu nhiên, nếu như $a+b=S$ và $ab=P$ thì $a, b$ là nghiệm của phương trình bậc nhì $x^2-Sx+P=0$

Ví dụ 2. Tìm nhì số thực $a, b$ biết tổng của bọn chúng vì như thế $2$ và tích của bọn chúng vì như thế $-3$

Lời giải:

Theo fake thuyết tớ với $a+b=2$ và $ab=-3$, khi bấy giờ $a, b$ là nghiệm của phương trình bậc nhì $x^2-2x-3=0 \Leftrightarrow x_1=3, x_2=-1$

Vậy nhì số $a, b$ cần thiết dò xét thứu tự là $3, -1$ hoặc $-1, 3$

Nhận xét: Phương trình bậc nhì $x^2-2x-3=0$ hoàn toàn có thể giải nhanh chóng vì như thế cách thức nhẩm nghiệm $1-(-2)+(-3)=0$ tương tự động như Ví dụ 1

#3. Tính độ quý hiếm biểu thức (biểu thức hoàn toàn có thể trình diễn trở nên nhiều thức đối xứng)

Ví dụ 3. Tính độ quý hiếm biểu thức $x_1^2+x^2$ biết $x_1, x_2$ là nghiệm của phương trình $7x^2+11x-13=0$

Thông thông thường khi đề bài bác đòi hỏi tính độ quý hiếm của biểu thức tuy nhiên độ quý hiếm này lại được xem trải qua nghiệm của phương trình thì tất cả chúng ta tránh việc giải phương trình  vì nghiệm thông thường thiếu thẩm mỹ.

Thay vô cơ tất cả chúng ta nên với gắng biến hóa biểu thức đang được mang lại trở nên những nhiều thức đối xứng rồi dùng lăm le lý Viet.

Lời giải:

Cách 1. Sử dụng lăm le lý Viet

Dễ thấy $x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2$

Mặc không giống $x_1, x_2$ là nghiệm của phương trình bậc nhì $7x^2+11x-13=0$ nên tớ với hệ thức $\left\{\begin{array}{ll}x_1+x_2&=\frac{-11}{7}\\x_1x_2&=\frac{-13}{7}\end{array}\right.$

Suy đi ra $x_1^2+x_2^2=(x_1+x_2)^2-2x_1x_2=\left(\frac{-11}{7}\right)^2-2\left(\frac{-13}{7}\right)=\frac{303}{49}$

Vậy => độ quý hiếm của biểu thức đang được nghĩ rằng $\frac{303}{49}$

Cách 2. Sử dụng PC CASIO

Tuy nghiệm của phương trình đang được mang lại thiếu thẩm mỹ tuy nhiên với sự tương hỗ của dòng sản phẩm tính CASIO fx-580VN X thì tất cả chúng ta vẫn hoàn toàn có thể tính được dễ dàng và đơn giản.

Chú ý: Cách này chỉ dùng nhằm đánh giá thành quả thôi nha chúng ta !

Bước 1. Chọn công thức đo lường và tính toán Equation / Func

Xem thêm: Báo VietnamNet

Bước 2. Chọn Polynomial

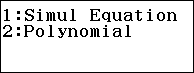
Bước 3. Chọn bậc của phương trình. Vì cần thiết giải phương trình bậc nhì nên bản thân tiếp tục ấn phím số 2

Bước 4. Lần lượt nhập những thông số của phương trình …

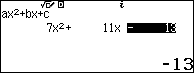
Bước 5. Nhấn phím = => nhấn phím STO => nhấn phím $(-)$

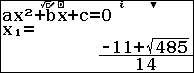
Bước 6. Nhấn phím = => nhấn phím STO => nhấn phím ${}^o~’~”$

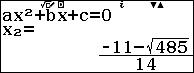
Bước 7. Chọn công thức đo lường và tính toán Calculate

Bước 8. Nhập biểu thức $A^2+B^2$ => nhấn phím =

Chú ý: Nếu nghiệm của phương trình đang được nghĩ rằng nghiệm phức thì ở Bước 7 tất cả chúng ta cần lựa chọn công thức đo lường và tính toán Complex

#4. Giải hệ phương trình đối xứng

Ví dụ 4. Giải hệ phương trình $\left\{\begin{array}{ll}x^2+y^2&=4\\x^3+y^3&=8\end{array}\right.$

Lời giải:

$\left\{\begin{array}{ll}x^2+y^2&=4\\x^3+y^3&=8\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}(x+y)^2-2xy&=4\\(x+y)^3-3xy(x+y)&=8\end{array}\right.$

Đặt $x+y=S, xy=P$ tớ được hệ phương trình $\left\{\begin{array}{ll}S^2-2P&=4\\S^3-3PS&=8\end{array}\right. \Leftrightarrow \left\{\begin{array}{ll}P&=-2+\frac{1}{2}S^2\\S^3-3\left(-2+\frac{1}{2}S\right)S&=8\end{array}\right.$

Giải hệ phương trình bên trên tớ được nhì nghiệm là $(-4, 6)$ và $(2, 0)$

Trường ăn ý 1 $x+y=-4, xy=6$

$x, y$ là nghiệm của phương trình $X^2+4X+6=0 \Leftrightarrow X^2+4X+6=(X+2)^2+2=0$

Như vậy => phương trình $X^2+4X+6=0$ vô nghiệm !

Trường ăn ý 2 $x+y=2, xy=0$

$x, y$ là nghiệm của phương trình $X^2-4X=0 \Leftrightarrow X(X-4)=0$

Suy đi ra phương trình $X^2-4X=0$ với nhì nghiệm là $0, 2$

Vậy => nghiệm của hệ phương trình đang được nghĩ rằng $(0,2)$ và $(2,0)$

Nhận xét:

• Nếu chúng ta có thể vẽ được nhì phương trình này lên nằm trong mặt mũi bằng phẳng tọa chừng Oxy thì nên dùng cách thức đồ dùng thị.
• Với Ví dụ 4 Phương pháp đồ dùng thị cũng là 1 trong lựa lựa chọn tối ưu.

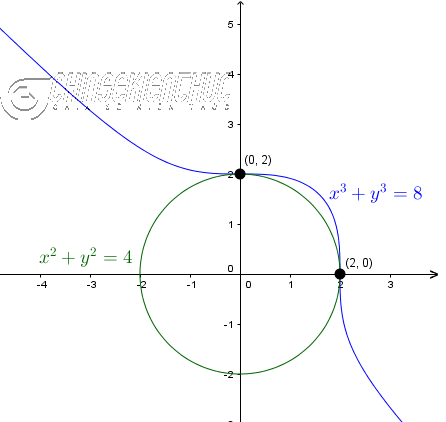
Quan sát đồ dùng thị tất cả chúng ta dễ dàng và đơn giản nhận ra bọn chúng với nhì phú điểm, tạo ra chừng của nhì phú đặc điểm này đó là nghiệm của phương trình đang được mang lại.

V. Lời kết

Vậy là tất cả chúng ta đang được hoàn thiện việc tuyên bố lại lăm le lý Viet, giống như việc áp dụng lăm le lý Viet vô giải một trong những dạng toán thông thường bắt gặp rồi ha,

Với những kỹ năng nền tảng tuy nhiên bản thân vừa mới được cung cấp/ ôn lại bên trên thì lúc này những bạn đã sở hữu thể thoải mái tự tin, tự động dò xét hiểu, tự động nghiên cứu và phân tích những mảng kỹ năng cao hơn nữa rồi đó. Xin Chào thân ái và hứa hẹn tái ngộ chúng ta trong mỗi nội dung bài viết tiếp theo sau !

Đọc thêm:

Xem thêm: Mùa thu Hà Nội: Những điều hấp dẫn giữa lòng thủ đô

• Định lý Pytago thuận, định lý Pytago hòn đảo và bài bác tập dượt ví dụ !
• Áp dụng định lý tổng phụ thân góc của một tam giác nhằm giải bài bác tập
• Định lý Talet vô tam giác, hệ quả định lý Talet và VÍ DỤ

CTV: Nhựt Nguyễn – Blogchiasekienthuc.com