fgate
fgate
Trang chủ Giáo Dục Công thức tính đường trung tuyến trong tam giác

Công thức tính đường trung tuyến trong tam giác

Tính hóa học đàng trung tuyến Toán 10

Công thức tính chừng nhiều năm đàng trung tuyến Toán 10 nhằm độc giả nằm trong tìm hiểu thêm. Bài ghi chép được tổ hợp nội dung kiến thức và kỹ năng của bài học kinh nghiệm về định nghĩa đường trung tuyến vô tam giác, đặc điểm đàng trung tuyến vô tam giác vuông, tam giác cân nặng, tam giác đều và công thức tính chừng nhiều năm đàng trung tuyến vô tam giác, mời mọc những em học viên nằm trong tìm hiểu thêm cụ thể và vận chuyển về nội dung bài viết sau đây nhé. Chúc chúng ta học hành tốt!

Bạn đang xem: Công thức tính đường trung tuyến trong tam giác

Bản quyền thuộc sở hữu VnDoc.
Nghiêm cấm từng kiểu dáng sao chép nhằm mục đích mục tiêu thương nghiệp.

1. Đường trung tuyến

- Đường trung tuyến của một đoạn trực tiếp là một trong những đường thẳng liền mạch trải qua trung điểm của đường thẳng liền mạch bại liệt.

- Đường trung tuyến vô tam giác là 1 đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của những cạnh đối lập nó. Mỗi tam giác đem 3 đàng trung tuyến.

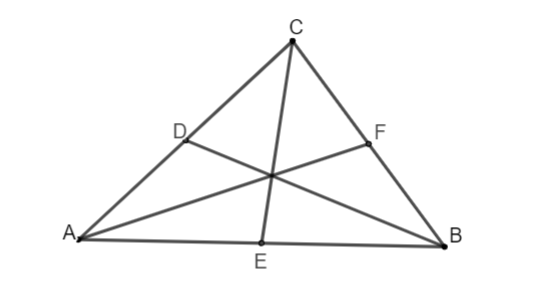
Ví dụ: Cho tam giác ABC, đem D, E, F theo lần lượt là trung điểm của những cạnh AC, AB, BC. Từ bại liệt tớ đem những đường thẳng liền mạch BD, AF, CE là những đàng trung tuyến của tam giác ABC.

Công thức tính đàng trung tuyến vô tam giác

2. Tính hóa học đàng trung tuyến vô tam giác

a. Tính hóa học đàng trung tuyến vô tam giác

- Ba đàng trung tuyến của tam giác đồng quy bên trên một điểm được gọi là trọng tâm.

- Khoảng cơ hội kể từ vô tâm cho tới từng đỉnh của tam giác vì chưng \frac{2}{3} đàng trung tuyến ứng với đỉnh bại liệt.

- Khoảng cơ hội kể từ vô tâm cho tới trung điểm từng cạnh vì chưng đàng \frac{1}{3} trung tuyến ứng với điểm bại liệt.

Ví dụ: Cho tam giác ABC, đem D, E, F theo lần lượt là trung điểm của những cạnh AC, AB, BC.

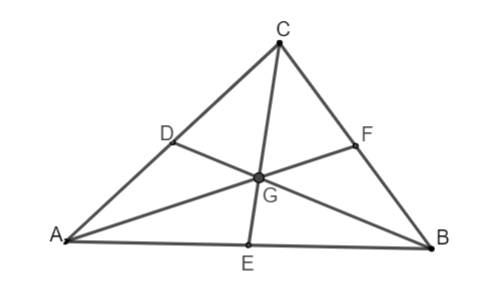Công thức tính đàng trung tuyến vô tam giác

- Gọi G là phó điểm của những đường thẳng liền mạch BD, AF, CE suy đi ra G là trọng tâm tam giác ABC.

Ta đem những đặc điểm sau:

\frac{{CG}}{{CE}} = \frac{{AG}}{{AF}} = \frac{{BG}}{{BD}} = \frac{2}{3}

\frac{{GE}}{{CE}} = \frac{{GF}}{{AF}} = \frac{{GD}}{{BD}} = \frac{1}{3}

b. Tính hóa học đàng trung tuyến vô tam giác vuông

- Đường trung tuyến của tam giác vuông đem những đặc điểm cộng đồng của đàng trung tuyến vô tam giác thông thường. Bên cạnh đó tớ đem những đặc điểm đặc thù sau:

+ Đường trung tuyến vô tam giác vuông ứng với cạnh huyền vì chưng 50% cạnh huyền.

Ví dụ: Cho tam giác ABC vuông bên trên C, đàng trung tuyến CD


+ Trong một tam giác đem đàng trung tuyến ứng với cùng một cạnh nhưng mà vì chưng 50% cạnh bại liệt thì tam giác này đó là tam giác vuông.

c. Tính hóa học đàng trung tuyến vô tam giác cân nặng, tam giác đều

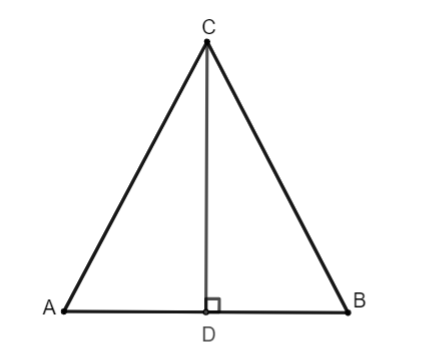
- Trong tam giác cân nặng, tam giác đều, đàng trung tuyến ứng với cạnh lòng thì vuông góc với cạnh bại liệt và phân tách tam giác trở thành nhị tam giác đều bằng nhau.

Ví dụ:

Công thức tính đàng trung tuyến vô tam giác

Xem thêm: Những tuổi nào hợp với năm Giáp Thìn 2024?

3. Công thức đàng trung tuyến

Cho tam giác ABC có tính nhiều năm những cạnh AB = c; AC = b; BC = a, những đàng trung tuyến {m_a};{m_b};{m_c}

4. Bài tập dượt ví dụ minh họa

Ví dụ 1:

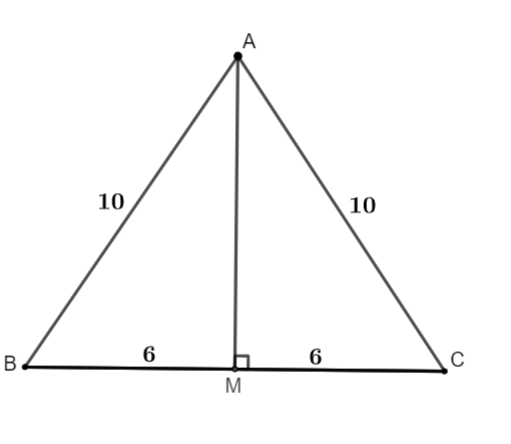
a. Tam giác ABC đem AB = AC = 10cm, BC = 12cm. Tính chừng nhiều năm đàng trung tuyến AM.

b. Tính chừng nhiều năm đàng trung tuyến AM của tam giác ABC đem góc \widehat {BAC} = {120^0}, AB = 4cm, AC = 6cm

Hướng dẫn giải

a.

Công thức tính đàng trung tuyến vô tam giác

Ta đem tam giác ABC cân nặng bên trên A, AM là trung tuyến suy đi ra AM là đàng cao, đàng phân giác của tam giác ABC

\Rightarrow BM = MC = \frac{1}{2}BC = 6

Áp dụng toan lý Pi – tớ – go cho tới tam giác vuông AMC có:

A{C^2} = A{M^2} + M{C^2} \Rightarrow AM = \sqrt {A{C^2} - M{C^2}} = 8

b.

Ví dụ 2: Cho tam giác ABC vuông bên trên A có tính nhiều năm hai tuyến phố trung tuyến AM và BN theo lần lượt vì chưng 6cm và 9cm. Tính chừng nhiều năm cạnh AB.

Hướng dẫn giải

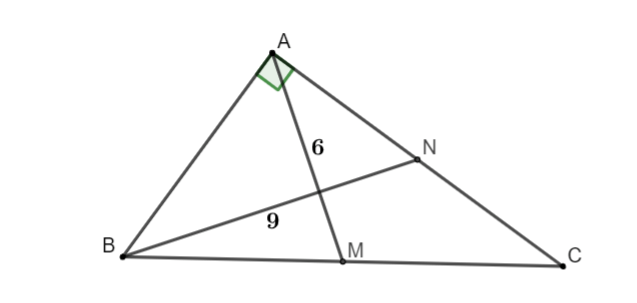
Công thức tính đàng trung tuyến vô tam giác

Tam giác ABC vuông bên trên A, AM là trung tuyến nên AM = BM = MC = 6

Suy đi ra BC = 12

Mặt khác:

\begin{matrix} \left\{ {\begin{array}{*{20}{c}} {A{M^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4}} \\ {B{N^2} = \dfrac{{B{C^2} + A{B^2}}}{2} - \dfrac{{A{C^2}}}{4}} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\dfrac{{A{B^2} + A{C^2}}}{2} = 72} \\ {\dfrac{{A{B^2}}}{2} - \dfrac{{A{C^2}}}{4} = 45} \end{array}} \right. \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {A{B^2} = 54} \\ {A{C^2} = 18} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {AB = 3\sqrt 6 } \\ {AC = 3\sqrt 2 } \end{array}} \right. \hfill \\ \hfill \\ \end{matrix}

Xem thêm: Xe đạp điện 5 triệu | 8 mẫu hot nhất thị trường 2023

-----------------------------------------------------------------------

Trên phía trên VnDoc đang được ra mắt cho tới chúng ta bài bác Công thức đàng trung tuyến Toán 10. Chắc hẳn qua chuyện nội dung bài viết độc giả đang được tóm được những ý chủ yếu na ná trau dồi được nội dung kiến thức và kỹ năng của bài học kinh nghiệm rồi đúng không nào ạ? Bài ghi chép tổ hợp những công thức đàng trung tuyến, định nghĩa đàng trung tuyến, đặc điểm đàng trung tuyến vô tam giác, kèm cặp Từ đó là những ví dụ, bài bác tập dượt rèn luyện đem điều giải cụ thể tất nhiên. Hy vọng với tư liệu này chúng ta học viên tiếp tục tóm cứng cáp kiến thức và kỹ năng áp dụng đảm bảo chất lượng vô giải bài bác tập dượt kể từ bại liệt học tập đảm bảo chất lượng môn Toán 10. Chúc chúng ta học tập đảm bảo chất lượng và ghi nhớ thông thường xuyên tương tác nhằm update được rất nhiều bài bác tập dượt hoặc có ích nhé!

Ngoài đi ra, để giúp đỡ độc giả nhận thêm nhiều tư liệu học hành hơn thế nữa, VnDoc ra mắt thêm thắt cho tới độc giả tìm hiểu thêm một vài ba tư liệu tương quan cho tới công tác lớp 10: Ngữ Văn 10, Tiếng Anh lớp 10, Vật lý lớp 10,... được VnDoc.com thuế tầm và tổ hợp.

  • Bài tập dượt công thức lượng giác lớp 10
  • Bảng công thức lượng giác sử dụng cho tới lớp 10 - 11 - 12
  • Giáo án ôn tập dượt hè môn Toán lớp 10

BÀI VIẾT NỔI BẬT

Lợi ích sức khỏe từ cải thìa: Ai nên ăn thường xuyên?

Cải thìa là một loại rau lá xanh có nhiều dưỡng chất thiết yếu cho hoạt động sống của cơ thể. Loại thực vật này chứa nhiều nước và rất giàu chất xơ. Dù là người bị tiểu đường, đang có vấn đề tiêu hóa hay tập luyện thể thao đều sẽ đạt được nhiều lợi ích sức khỏe nếu ăn cải thìa thường xuyên.